The Chair of Cyber-Physical-Systems

The Chair of Cyber-Physical-Systems at the Montanuniversität Leoben in Austria is headed by Prof. Elmar Rueckert.
The group’s research topics are autonomous systems, machine and deep learning, embedded smart sensing systems, and computational models.
Latest Research Videos

Slide
ROMR

NavAcl-Q+

ROMR

TacProMPs

NavACL-Q







AI & Robotics Positions and Topics
The chair is offering a number of open positions and student thesis topics in AI and robotics.
Also check our wiki, which offers numerous public posts on open source code repositories or tutorials.
Latest news
News
April 5, 2024
Conference Paper Accepted at UR 2024
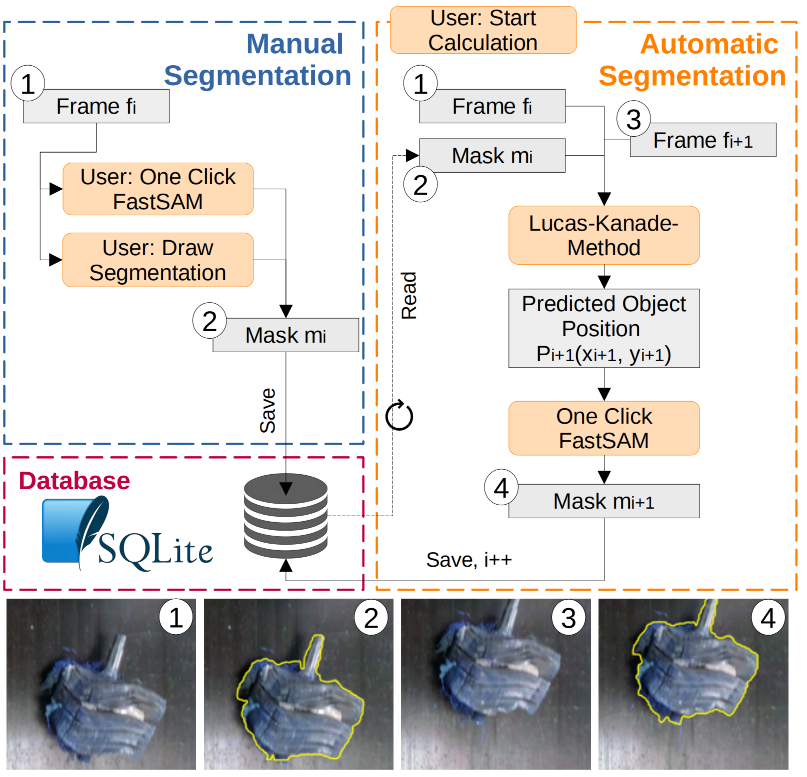
The paper on ‘Semi-Autonomous Fast Object Segmentation and Tracking Tool for Industrial Applications‘ by Melanie Neubauer and Elmar Rueckert was accepted for publication in the International Conference on Ubiquitous Robots..Read MoreApril 5, 2024
Conference Paper Accepted at UR 2024
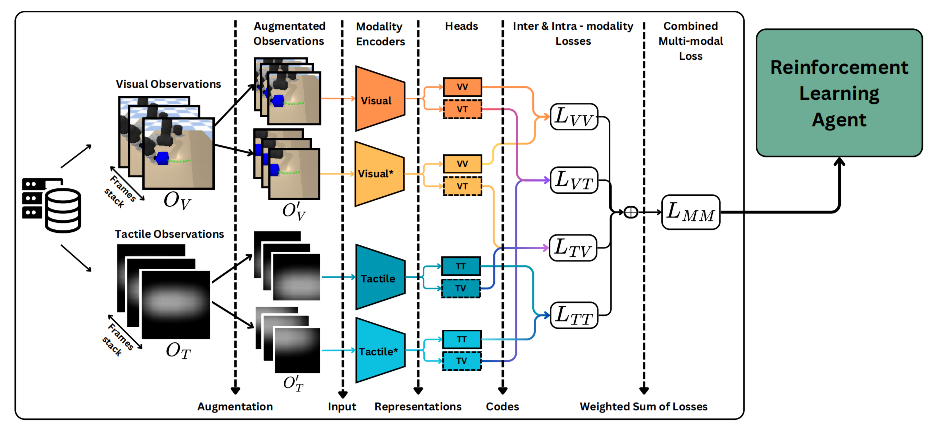
The paper on ‘M2CURL: Sample-Efficient Multimodal Reinforcement Learning via Self-Supervised Representation Learning for Robotic Manipulation‘ by Fotios Lygerakis, Vedant Dave and Elmar Rueckert was accepted for publication in the International..Read MoreApril 5, 2024
Conference Paper Accepted at UR 2024
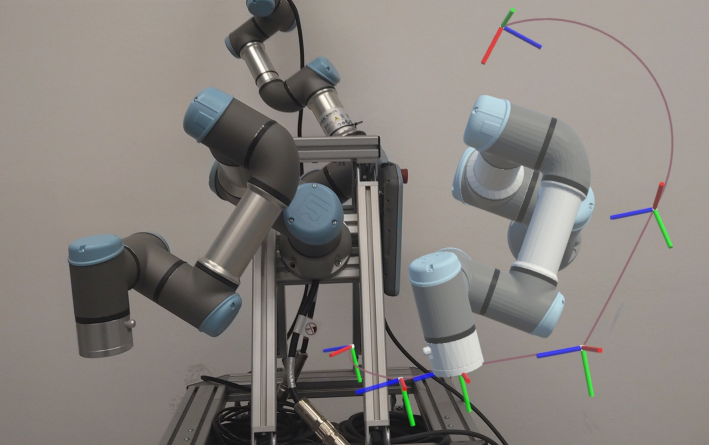
The paper on ‘Advancing Interactive Robot Learning: A User Interface Leveraging Mixed Reality and Dual Quaternions‘ by Nikolaus Feith and Elmar Rueckert was accepted for publication in the International Conference..Read MoreApril 5, 2024
Conference Paper Accepted at UR 2024
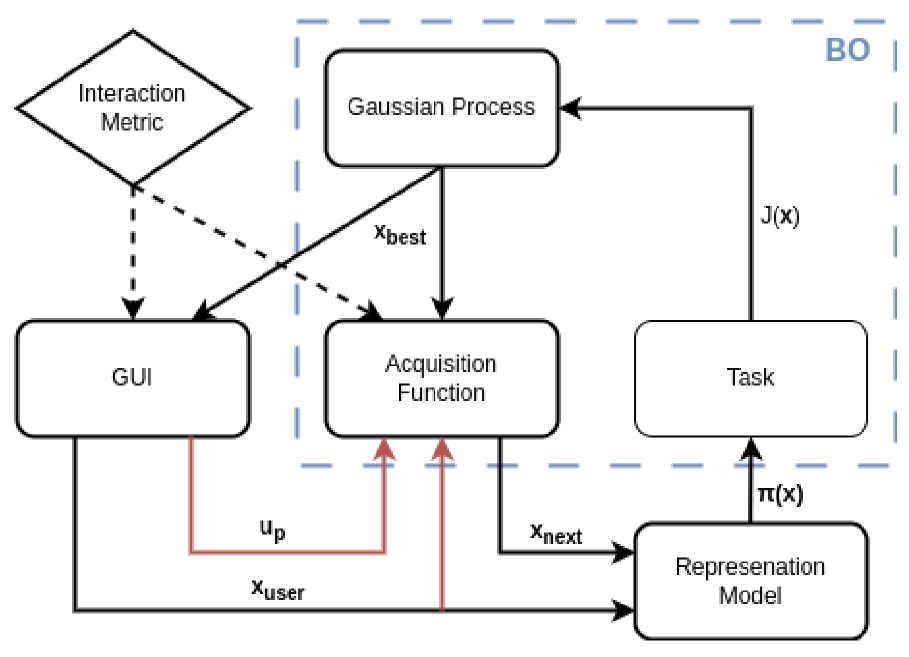
The paper on ‘Integrating Human Expertise in Continuous Spaces: A Novel Interactive Bayesian Optimization Framework with Preference Expected Improvement‘ by Nikolaus Feith and Elmar Rueckert was accepted for publication in..Read MoreFebruary 27, 2024
Journal Paper accepted at Sensors (MDPI)
The paper by Kunavar, T., Jamšek, M., Avila-Mireles, E. J., Rueckert, E., Peternel, L., and Babič J. on “The Effects of Different Motor Teaching Strategies on Learning a Complex Motor..Read MoreFebruary 2, 2024
Conference Paper Accepted at ICRA 2024
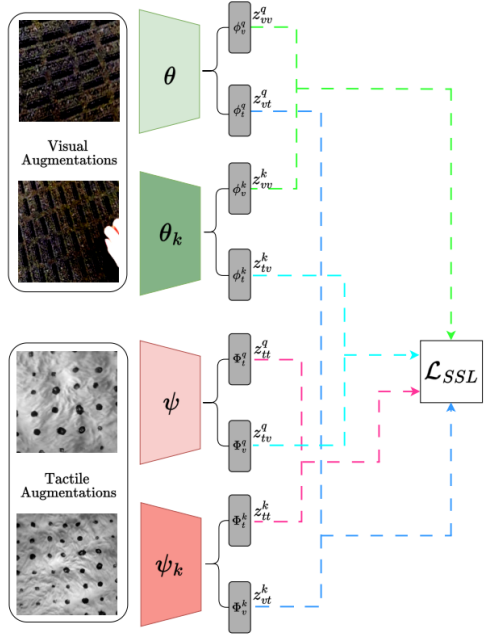
The paper on ‘Multimodal Visual-Tactile Representation Learning through Self-Supervised Contrastive Pre-Training‘ by Vedant Dave*, Fotios Lygerakis* and Elmar Rueckert was accepted for publication in the IEEE International Conference on Robotics and..Read MoreJanuary 16, 2024
Conference Paper accepted at HRI 2024
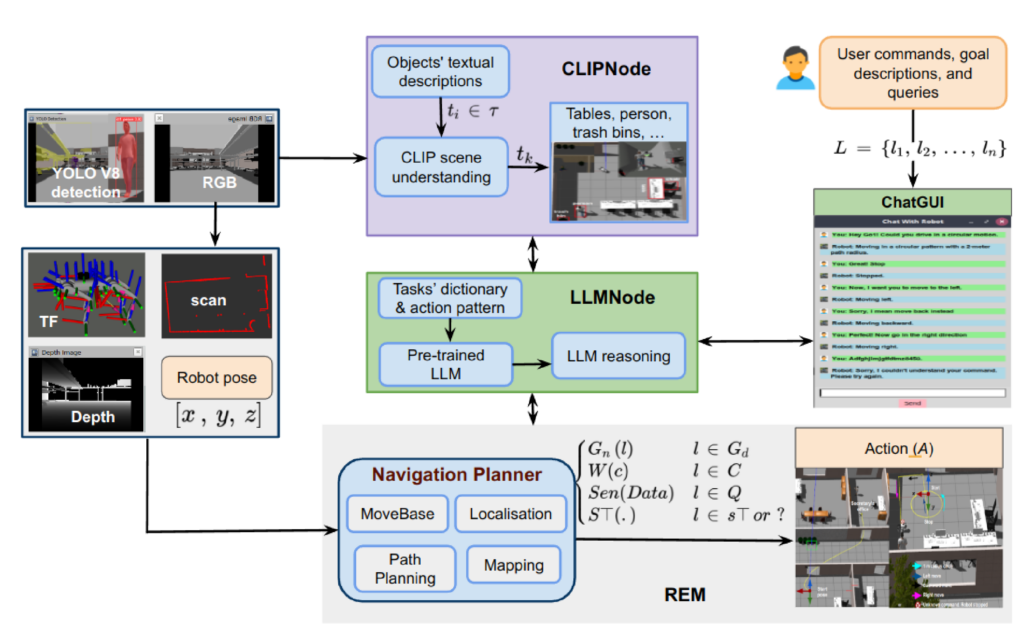
The paper on ‘The Conversation is the Command: Interacting with Real-World Autonomous Robot Through Natural Language‘ by Linus Nwankwo and Elmar Rueckert was accepted for publication the the International Conference..Read MoreNovember 10, 2023
FFG Project Grant – NNATT
Our joint proposal on “Sustainable use of excavated materials from civil engineering and tunnel construction using sensor-based technologies” was granted by the Austrian Research Promotion Agency (FFG). The project starts..Read MoreAugust 25, 2023
Conference Paper accepted at ACAIT 2023
The paper on ‘CR-VAE: Contrastive Regularization on Variational Autoencoders for Preventing Posterior Collapse‘ by Fotios LYgerakis and Elmar Rueckert was accepted for publication at the Asian Conference of Artificial Intelligence..Read MoreJuly 10, 2023
Conference Paper accepted at ICSTCC 2023
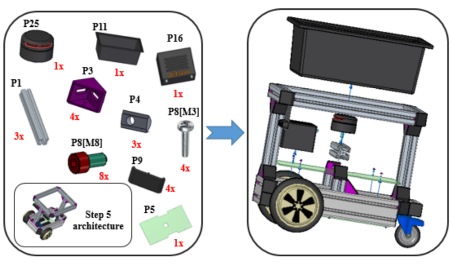
The paper on Deep Reinforcement Learning for Mapless Navigation of Autonomous Mobile Robot by Yadav, Harsh; Xue, Honghu; Rudall, Yan; Bakr, Mohamed; Hein, Benedikt; Rueckert, Elmar; Nguyen, Ngoc Thinhwas accepted..Read MoreMarch 13, 2023
Conference Paper accepted at RAAD 2023
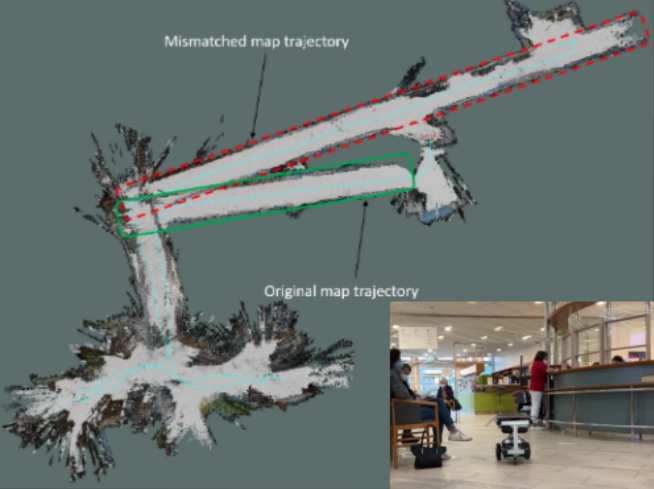
The paper on Understanding why SLAM algorithms fail in modern indoor environments by Linus Nwankwo and Rueckert Elmar was accepted for publication at the International Conference on Robotics in Alpe-Adria-Danube..Read MoreJanuary 13, 2023
FFG Project Grant – KIRAMET
Our joint proposal on “AI for recycling 2022” (germ. Künstliche Intelligenz für Recycling 2022) was granted by the Austrian Research Promotion Agency (FFG). The project starts in March/April 2023 and..Read MoreSeptember 29, 2022
Conference Paper accepted at HUMANOIDS 2022
The paper on End-To-End Deep Reinforcement Learning for First-Person Pedestrian Visual Navigation in Urban Environments by Honghu Xue, Rui Song, Julian Petzold, Benedikt Hein, Heiko Hamann and Rueckert Elmar was..Read MoreMore news on Professor Rueckert’s page.